Elektrická pole v erupcích a protuberancích
Abstrakt
Elektrické pole patří k těm fyzikálním projevům hmoty, o jejichž přítomnosti a důležitosti v astrofyzikální plazmě nejsou žádné pochybnosti. Přesto, že vliv elektrických polí na emitované elektromagnetické záření je teoreticky podložen a v laboratorních podmínkách dostatečně ověřen, nedaří se zatím veličiny elektrického pole ve sluneční plazmě spolehlivě, prokazatelně a opakovaně měřit. Článek uvádí přehled problematiky projevů a možností detekce elektrických polí v plazmě slunečních erupcí a protuberancí. Jsou též uvedeny vlastní zkušenosti při pozorování na elektrografu, který byl instalován na velkém koronografu observatoře Sacramento Peak.
Úvod
Elektrické pole (jako každé jiné fyzikální pole) je formou hmoty, která má jiné vlastnosti než látka a lze ji v každém bodě prostředí popsat pomocí fyzikálních veličin. V daném případě se jedná zejména o intenzitu elektrického pole, jejíž směr je stanoven konvencí. Je definována jako síla, kterou pole vytvořené kolem náboje působí na testovací těleso nabité jednotkovým kladným nábojem. Je závislá na velikosti elektrického náboje vytvářejícího pole, na druhé mocnině vzdálenosti od tělesa a na vlastnostech prostředí kolem tělesa.
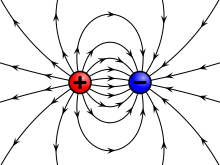
Elektrické pole v okolí kladného a záporného náboje.
Náboj, který není v pohybu, vytváří pole elektrostatické, pohybující se náboj vytváří pole elektrodynamické. V něm se mění elektrická intenzita v čase a to způsobuje vznik pole magnetického. Stejně tak změna magnetického pole vede ke vzniku pole elektrického. Tyto vzájemné vztahy veličin obou polí popisují Maxwellovy rovnice obecného elektromagnetického pole.
Elektrická pole jsou v mikrosvětě i v makrosvětě přítomná tam, kde existuje separace elektrických nábojů, nebo proměnné pole magnetické. Elektrické pole je také neoddělitelnou složkou pole elektromagnetického. S ním se setkáváme v různých formách. Např. ve formě vlnění/záření. Rovnice popisující vlnění elektromagnetického pole je implicitně obsažena v Maxwellových rovnicích. A tak i viditelné světlo je elektromagnetickým zářením, tedy projevem kmitů elektromagnetického pole o určitých frekvencích/vlnových délkách. A podobně také vysokoenergetické záření kosmického původu, či např. radiový signál nebo šum od přístrojů vytvořených člověkem.
Pod přirozeným elektrickým polem si nejspíše vybavíme školní pokus z elektrostatiky, kdy vlasy spolužačky po nabití Van de Graafovým generátorem vytvořily kolem její hlavy svatozář. Každý známe výboje atmosférické elektřiny při bouřce doprovázené světelnými a zvukovými projevy, výboj na hrotech hřebene při rozčesávání vlasů, jiskry při svlékání svetru ze syntetických materiálů a obecně při tření vhodných suchých a neuzemněných izolantů. I solární panely, jimiž jsou dnes zapleveleny i úrodné české a moravské lány, jsou založeny na separaci kladného a záporného náboje v polovodiči a jeho zužitkování pro výrobu elektřiny na principu fotovoltaického jevu. A mohli bychom zmiňovat využití rozdílu elektrických potenciálů při rozvodu elektrické energie a nesčetné další množství projevů či využití elektrického pole. Podstatné je, že elektrické/elektromagnetické pole a jevy s ním spojené vždy souvisí s akumulací, uvolněním, či přenosem energie. To platí zejména v makrosvětě, zatímco při studiu mikrosvěta bychom poznali, že síly elektrické drží vše pohromadě a vděčíme jim za to, že můžeme svět doslova vidět jaký je. Ve všech zmíněných případech makrosvěta i mikrosvěta se ale jedná o řádově naprosto nesouměřitelné hodnoty charakteristických veličin elektrického pole.
Pro energii fotonu platí E = h × ν = hc/λ, kde Planckova konstanta je h = 6,626×10-34 J s. Je-li hodnota c= 299 792 458 ms-1, a vlnová délka ve viditelném oboru pro čáru Hα je λ = 6562,8×10-10 m, pak příslušný foton má energii E = 3,026×10-19 J, což je ekvivalentní 1,888 eV (1 J = 6,241×1018 eV). Celková energie, jejíž převážná část má charakter energie elektromagnetické, uvolněná při největších pozorovaných slunečních erupcích dosahuje hodnot E = 1025 J. Setkáváme se tedy s poměrem energií až 44 řádů. Tento velký rozsah energií obsahuje všechny elektromagnetické jevy, které bychom mohli zkoumat a zejména fyzikálně měřit. Pokud jde o měření elektrických polí na Slunci a obecně ve Vesmíru, jediným poslem, který nám informace přináší až na Zemi do našich měřících přístrojů, je elektromagnetické záření. Zatímco v elektrotechnice můžeme měřit veličiny elektrického pole galvanometrem a podobnými přístroji, k rozšifrování skrytého poselství o vesmírných elektrických polích nám nepomohou. Musíme nejdříve pochopit, jakým způsobem ovlivňují elektrická pole fotony v prostředí jejich vzniku a šíření a pak vypracovat metodiku odvození potřebných veličin z pozorování.
Z veličin, popisujících elektrické pole, pro účel tohoto pojednání zmíníme elektrický potenciál a napětí. Elektrický potenciál daného místa neměnného elektrického pole je roven množství práce potřebné pro přenesení jednotkového elektrického náboje ze vztažného bodu s nulovým potenciálem do daného místa. Elektrické napětí je pak rozdíl elektrických potenciálů ve dvou bodech pole. Jde tedy o množství práce vykonané/spotřebované elektrickými silami při přemísťování kladného jednotkového náboje mezi dvěma body pole. Jednotkou elektrického potenciálu i elektrického napětí v soustavě SI je jeden Volt. Intenzitu elektrického pole pak měříme v jednotkách Volt na metr [V/m]. Rozměrově je to vlastně gradient či spád elektrického potenciálu nebo napětí. Tato veličina se měří při analýze elektrických polí na Slunci. Pro konkrétní představu lze uvést typické hodnoty intenzity elektrického pole v aplikacích mikro a nanotechniky, kde se setkáváme s malými vzdálenostmi mezi vodiči. V polovodičích jsou běžné hodnoty intenzity elektrického pole řádu 1 V na µm.
Dosud nejúplnějším přehledem problematiky elektrických polí ve sluneční atmosféře je práce Foukala a Hinaty (1991). Jejich článek se zabývá jak otázkou možností detekce elektrických polí, tak mechanismy, které k vytvoření elektrických polí ve sluneční atmosféře mohou vést. Daná problematika je zajímavá i z hlediska výzkumu mechanismu ohřevu plazmy ve slunečních erupcích. Fyzikální procesy ve sluneční plazmě jsou natolik dynamické, že elektrická pole se musí projevovat a hrát v nich nezanedbatelnou roli. Ať již se jedná o elektrická pole na úrovni atomární nebo makroskopické. Některé procesy mohou být zdrojem polí stejnosměrných, vyvolaných gradientem hustoty nebo pohybem elektricky vodivé plazmy v magnetickém poli či časovou změnou magnetického pole. Vznik a vlastnosti elektrických polí si můžeme představit při praktickém uplatnění dvou Maxwellových rovnic:
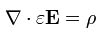
Rovnice říká, že siločáry elektrického pole o intenzitě E začínají a končí v tom místě prostoru, kde je soustředěn elektrický náboj. Zdrojem elektrického pole je tedy volný náboj s hustotou ρ, ε je elektrická permitivita materiálu/prostředí.
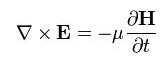
Tato rovnice říká, že při časové změně magnetického pole je elektrické pole vírové (siločáry jsou uzavřené) a podél vírů je možno měřit napětí. H je intenzita magnetického pole a μ je magnetická permeabilita materiálu/prostředí.
Čistě matematickými úpravami lze z Maxwellových rovnic přímo odvodit rovnici vlnění pro vektor intenzity elektrického pole:
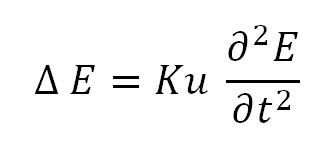
Vezmeme-li v úvahu různé varianty chování veličin popisujících elektromagnetické pole, dospějeme i k možnostem generace střídavých elektrických polí, které lze popsat právě rovnicí vlnění. Střídavá elektrická pole mohou být produktem vysoko- nebo nízkofrekvenčních plasmových oscilací a dalších dynamických periodických jevů v turbulentní sluneční plasmě.
Možnosti detekce elektrických polí ve sluneční atmosféře jsou mnohem komplikovanější, než je tomu u pole magnetického. Je to dáno hlavně tím, že vlivy zmíněných typů elektrických polí na elektromagnetické záření se kombinují a mohou se prolínat jednak mezi sebou navzájem a jednak s vlivy dalšími. Zářící atom v elektrickém poli lze přirovnat k chování oscilátoru rušeného vnějšími vlivy. Pokud je těchto vlivů více, je velice obtížné příznaky jednotlivých vlivů navzájem odlišit. Jediným vodítkem musí být fyzikální úvahy interpretátora a jeho „fyzikální cit pro realitu ve zkoumaném prostředí“. Je proto samozřejmé, že úsilí po dosažení detekce elektrických polí se jednak koncentruje do situací, kde se předpokládá největší dopad na záření, a jednak tyto situace musí být z hlediska reálného fyzikálního modelu co možná nejjednodušší. Pak mohou mít největší naději na pozitivní výsledek.
Vliv elektrického pole na zářící atom
V elektrickém poli, nebo při vzájemném pohybu prostředí a magnetického pole dochází v závislosti na míře elektrické vodivosti prostředí k polarizaci nábojů, resp. ke vzniku elektrického proudu. V některých příznivých případech, lze odraz těchto jevů detekovat v záření vycházejícím z daného prostředí. Formálně odlišujeme dvě skupiny procesů. Jednou z nich jsou vlivy elektrického pole na úrovni mikroskopické, tj. interatomární, resp. intermolekulární a druhou pak vlivy elektrického pole makroskopického. V každém případě jde o výpočet vlivu elektrické síly na zářící atom a dopad tohoto vlivu na emitovaný nebo absorbovaný foton. Každý atom sestává z jádra s elektricky kladným nábojem a z elektricky záporného elektronového obalu. Pokud je takový atom vystaven působení elektrického pole, měl by reagovat polarizací, tj. posunem těžišť svého kladného jádra a záporného obalu podél směru působící elektrické síly. Tato síla má charakter poruchy působící na procesy v atomu. Poruchu je možné zahrnout do výpočtu řešení Schrodingerovy vlnové rovnice a nalézt řešení zahrnující efekty spojené s poruchou.
Základním úkolem je popsat charakter výsledné působící rušivé elektrické síly. Tato síla zpravidla závisí na množství a typu atomů a iontů, které se pružných srážek, nebo obecně poruch, zúčastňují. Pro jednotlivé modelové situace je tedy síla a následné řešení implicitní funkcí hustoty částic a také teploty. Pro výpočty se zavádí modely harmonického oscilátoru, případně kvazistatického stavu.
V první skupině jevů rozlišujeme statistické rozšiřování čar, nebo rozšiřování čar útlumem v důsledku pružných srážek zářících atomů s okolními elektrony nebo ionty. Pro jednoduchost se vždy předpokládá přiblížení odpovídající takovému modelu, kdy se vyzařující nebo absorbující atom chová jako jednoduchý harmonický oscilátor bez rušivé síly. Tento stav se poruší tehdy, jestliže na atom krátkodobě zapůsobí rušivá síla v důsledku pružné srážky s okolním iontem nebo elektronem. To má za důsledek změnu fáze, případně amplitudy harmonických kmitů. V analogii zářícího atomu pak dochází k malému posunu příslušné energetické hladiny' atomu. Tento posuv můžeme vyjádřit změnou energie, nebo přímo změnou frekvence příslušného fotonu. Výsledná změna frekvence Δν vyzářeného, nebo absorbovaného fotonu je pak dána obecným vztahem:
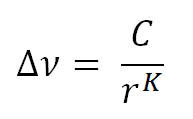
Kde C je konstanta, r je vzdálenost těžišť emitujícího (resp. absorbujícího) atomu a rušící částice (iontu), K je exponent vyjadřující charakter působení rušivé síly elektrického pole.
Rozšiřování čar vodíku a některých čar u prvků vodíku podobných můžeme popsat stavem K = 2, kdy jde o tzv. lineární Starkův jev. Při něm je výsledná síla přímoúměrná působící Coulombovské síle a rušícími částicemi jsou ionty. U atomů jiných prvků se lineární Starkův jev vyskytuje jen při velmi silných elektrických polích, zatímco při slabých polích se projevuje kvadratický Starkův jev.
Je-li K = 4, jde o kvadratický Starkův efekt. Rušící síla způsobující rozšíření energetické hladiny v atomu je úměrná druhé mocnině Coulombovské síly a rušení je působeno útlumem v důsledku srážek atomů s elektrony. Dále při kvadratickém Starkově jevu dochází k výskytu čar porušujících výběrové pravidlo pro orbitální kvantové číslo 1. Čím je zářící atom, nebo iont komplikovanější, tím složitější je i řešení kvadratického Starkova jevu. Proto tento jev nebyl dosud zcela prostudován. Druhá skupina zkoumaných jevů vychází z představy kvazistatického rozdělení elektrických polí v důsledku pomalu se pohybujících iontů. Tato elektrická pole vedou také k rozštěpení energetických hladin v atomu a v konečném důsledku bud k rozšíření nebo deformování profilu spektrální čáry. Předpokládá se, že každý iont má vlastní rozdělení elektrického pole:
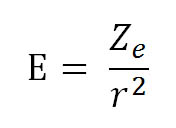
které je nezávislé na ostatních iontech a elektronech plazmy. Zde je r vzdálenost od iontu s nábojem Ze. Střední vzdálenost mezi ionty je r0 = (4πNi/3)-1/3, kde Ni je hustota iontů. Z těchto vztahů vypočteme střední intenzitu elektrického pole E0 = Ze/(r0)2 = 2,61 Ze (Ni)2/3 v blízkosti testovacího atomu. Další postup spočívá ve výpočtu funkce pravděpodobnosti, že zářící nebo absorbující atom je ovlivněn elektrickým polem nejbližšího iontu, případně polem více okolních iontů. Za předpokladu, že r0 je menší než debyeovský poloměr rD = 6,90/(T/Ni)1/2 se tato pravděpodobnost řídí tzv. Holtzmarkovou rozdělovací funkcí závisející na intensitě kvazistatického elektrického pole E, zprostředkovaného ionty. Zde T je kinetická teplota plazmy. Pro atomy vodíkového typu nastává lineární Starkův jev a frekvence νmn ("ný" s idexem "mn") odpovídající přechodu mezi hladinami s hlavními kvantovými čísly m a n se rozštěpí na množství podhladin. Ty jsou od původní hodnoty νmn neporušeného stavu vzdáleny o Δ νmn, pro něž platí:
Δ νmn=1,92 × 106 (E/Z) Xmn [Hz]
kde koeficient X = m(m2-m1)-n(n2-n1) je funkcí kvantových čísel m1, m2, nl a n2, která mohou nabývat celočíselných hodnot 0 až m-1 a 0 až n-1. Přitom rozměr jednotek intenzity elektrického E je ve V/cm. Celkové rozšíření čáry odpovídající přechodu mezi hladinami m a n je dáno superpozicí všech příslušných Starkovských komponent Δ νmn, kde je ještě nutno započíst váhu každé z nich. Jednotlivé podhladiny starkovsky rozštěpených čar o jim odpovídající síly oscilátorů pro nejdůležitější čáry sérií vodíku jsou publikovány v práci Underhill a Waddel (1959).
V souhrnu lze konstatovat, že elektrické pole působící na atom způsobí rozštěpení původně složených hladin elektronů na množství podhladin. V případě velkého rozštěpu bychom mohli pozorovat rozštěp spektrální čáry na několik komponent. Zpravidla však pozorujeme rozšíření nebo deformací profilu čáry. Pro možnosti detekce je podstatná polarizace jednotlivých skupin pí a sigma komponent.
Uvažujeme-li, že směr elektrického pole je kolmý na směr pozorování, pak je možno v pozorovaném záření detekovat dva systémy lineárně polarizovaných komponent. Pí-komponenty jsou polarizovány podél vektoru elektrického pole a sigma komponenty napříč pole. Systém sigma-komponent leží blíže středu neporušené čáry, zatímco systém pí-komponent se nachází dále v křídlech příslušné čáry. Použijeme-li systém měření lineární polarizace přicházejícího Starkovsky rozšířeného čárového profilu, můžeme získat informaci o směru elektrického pole příčného k pozorovací přímce.
Typy elektrických polí ve slunečním plazmatu
Uvažujme o typech a zdrojích elektrických polí, která se mohou vyskytovat ve sluneční atmosféře. S odvoláním na dříve uvedené Maxwellovy rovnice, vlnovou rovnici a vztahy pro coulombovskou sílu můžeme konstatovat, že mohou být elektrostatického, indukčního, vlnového, nebo dynamického původu.
Shodně s členěním v článku Foukala a Hinaty (1991) vyjmenujeme hlavní typy a zdroje slunečních elektrických polí a případný odhad velikostí těchto polí.
A - elektrická pole paralelní s vektorem magnetického pole
V podfotosférických vrstvách se pomocí pohybů plazmy v příčném magnetickém poli generují proudy, které pak vzplývají podél magnetických siločar do koróny. V koróně pak způsobují elektrické pole řádově 10-7 V/cm, což je hodnota, jež se nedá dálkovým sondováním měřit.
Podle Alfvénova-Carlquistova modelu, dochází k erupci při přerušení elektrického proudu protékajícího obloukovou smyčkou a následně dojde k poklesu potenciálu na velmi krátké vzdálenosti. Přitom se vytvoří dvojitá proudová vrstva, jež má průměr jen několik debyeovských délek. Elektrické pole pak může pro teploty a hustoty obvyklé v chromosférické erupci dosahovat řádu 1010 V/cm. Tloušťka jedné této elektrizované vrstvy a tudíž i míra pozorovatelné emise však natolik malá, že vliv tohoto jevu se při pozorování neprojeví. Naděje na pozorování by vzrostla, pokud by se jednalo o filamentarizovaný jev, tzn. proudová vrstva, by byla mnohonásobná a míra emise by úměrně tomu vzrostla.
K dalším zdrojům elektrického pole ve sluneční erupci počítáme svazky vysokoenergetických elektronů nebo protonů. Ty mohou být vystřelovány z koróny magnetickou erupční smyčkou proti chromosféře a fotosféře tak vyvolat vyrovnávací elektrické pole a návratové proudy. Hustota návratového proudu je tak veliká, že může způsobit plazmové nestability. Podle odhadu by měl energetický svazek, který je schopen způsobit záblesk tvrdého X záření, vyvolat kvazistatické elektrické pole kolem 50 V/cm. Toto pole pak má za následek vyrovnávací návratový proud. Časová škála tohoto jevu je asi do 100 s, což opět velmi snižuje pravděpodobnost detekce. Šance pro zachycení se zvyšuje s možností opakování celého procesu v počáteční fázi erupce.
Předpokládá se, že silné elektrické proudy vznikají nad erupčními smyčkami v neutrální vrstvě orientované podél osy fotosférické neutrální čáry magnetického pole. Tyto proudy a s nimi spojená elektrická pole by měly být kolmé k systému erupčních smyček a tedy přibližně rovnoběžné s osou kanálu dvouvláknové erupce. Podle odhadu by hodnota těchto polí měla činit asi 20 V/cm. Pokud tedy míra emise z těchto oblastí byla dostatečná, pak je tato úroveň pole detekovatelná.
B - elektrická pole kolmá k magnetickému poli
Zdrojem elektrodynamické síly ve sluneční atmosféře může být pohyb vodivé plazmy napříč magnetického pole B. Tento pohyb může být vyvolán gravitační, odstředivou, Corriolisovou, nebo jinými druhy sil. Může být rovněž spontánní, pokud se jedná o difusi nebo rekonexi opačně orientovaných magnetických polí. První druh situace může nastat např. tehdy, když plazma proniká napříč magnetickým polem v klidné protuberanci, v koronálním dešti nebo obecně v plazmatické smyčce. Druhé situace by měly nastat při rychlých rekonexních procesech, při nichž dojde ke zjednodušení magnetické konfigurace a magnetická pole se vlastně propojují přes vodivou plazmu jiným způsobem.
Interpretace Starkova jevu při těchto konfiguracích je velmi přímočará. Vlastní procesy generující tato pole jsou však natolik složité, že odhad velikosti elektrických polí a možností jejich detekce je naprosto otevřenou oblastí.
C - časově proměnná elektrická pole
Časově proměnná elektrická pole jsou generována proměnnou indukcí, jako je tomu u elektromagnetických vin, např. Alfvénových. Jinou možností je časově proměnné rozdělení elektrického náboje, jako jsou elektrostatické viny, např. plazmové oscilace. Konkrétních vlnění, která přicházejí v úvahu, je celá řada a mohou se vyskytovat v širokém rozmezí od slunečního nitra, přes atmosféru až po daleký meziplanetární prostor. Odhady velikostí efektivních hodnot těchto časově proměnných elektrických polí jsou od zcela zanedbatelných hodnot až po řádově kV/cm. Stejně jako v předchozích případech zůstává základní podmínkou pro detekci takových polí dostatečná míra emise a časová škála srovnatelná s prací detekční techniky.
Způsoby detekce elektrického pole dálkovým sondováním
Je samozřejmé, že měřit elektrická pole na Slunci přímou sondáží nepřichází v úvahu a musíme se spolehnout na metody dálkového sondování. Jediným způsobem detekce elektrických polí na Slunci je rozbor slunečního spektra v některých čarách, které jsou na elektrická pole sensitivní.
Nejjednodušší způsob výpočtu intenzity elektrostatického pole v zářící plazmě je založen na interpretaci dříve uvedeného Holtzmarkova vztahu E = 2,61 Ze (Ni)2/3 pro rozšíření profilů čar Balmerovy série vlivem tlaku částic. Vztah platí pro okolí zářícího atomu ovlivněného středním elektrickým polem okolních nabitých částic. Pokud jsme schopni nezávislou metodou určit hustotu iontů Ni, pak můžeme vypočítat hodnotu E. Naopak z odhadu hodnoty elektrického pole E, můžeme vypočítat hustotu iontů, resp. elektronů. Přehled hodnot dosažených podle tohoto vztahu nalezneme např. v publikaci Švestky (1976).
Vysoká hodnota intenzity elektrického pole byla naměřena Davisem (1977) v erupci na limbu a v erupčních smyčkách. Davis interpretoval nalezený posuv heliové čáry 3705 Å jako vliv kvadratického Starkova jevu způsobeného polem o intenzitě 700 V/cm. Davis uvádí, že měření se vztahuje k pozdní fázi erupce, elektronová teplota plazmy byla určena na 35 000 K, celková hustota částic N = 8×1011 cm-3. Ještě vyšší hodnotu hranice elektrického pole 1400 V/cm uváděli na základě deformace profilu heliové čáry 4026 Å Lites a kol. (1986). Vypouklinu na profilu interpretovali jako zakázanou čáru vyvolanou kvadratickým Starkovým jevem. Interpretace dolíčků, resp. vypouklin na profilech čar jako projev přerozdělení energie v čáře v důsledku vlivu elektrických polí na zářící atom, se v literatuře nacházejí poměrně často. Např. Oks (1978) dospěl k hodnotě kvazistatického elektrického pole řádově 100 V/cm vyvolaného elektronovými oscilacemi v zářící plazmě erupce. Firstová a kol. znovu změřili originální spektra Balmerových čar H7 a H11, jež Oks použil a ukázali, že deformace profilů nelze jednoznačně takto interpretovat.
Jiný způsob detekce elektrických polí v erupcích aplikoval Drawins (1973). Snímal sluneční erupce pomocí úzkopásmového H-alfa filtru ve dvou ortogonálních lineárních polarizacích, aby zkoumal změny šířky čáry odpovídající pí a sigma komponentám polarizovaného záření v čáře. Tyto komponenty se musí vyskytovat ve směru podél a napříč vektoru elektrického pole v plazmě podobně jako je tomu u Zeemanova jevu. Citlivost použité metody pro čáru Hα byla velmi nízká (na úrovni 1000 V/cm). Metoda byla navíc ovlivněna různými přístrojovými efekty.
Údaje o naměřených hodnotách elektrického pole v různých jevech sluneční aktivity zpravidla nebyly potvrzeny novými nebo opakovanými měřeními. To dokládá komplikovanost dané problematiky po stránce teoretické, pozorovací i interpretační. K potlačení některých vlivů a k zlepšení možností jednoznačné interpretace bylo užito modelových situací v jevech sluneční aktivity nad slunečním limbem. Jedná se především o erupční smyčky, spreje a aktivní protuberance. Foukal a kol. (1983) odvodili ze starkovského rozšíření Balmerových čar hodnotu celkového elektrického pole v erupčních smyčkách okolo 170 V/cm. Hodnota makroskopického elektrického pole v rozsahu 40 V/cm byla nalezena rovněž v erupční smyčce Foukalem a kol. (1986). Z úvah o možných hodnotách hustoty ve smyčce 1012 až 1013 cm-3 vyplývá, že vrstva plazmy emitující starkovsky rozštěpené záření má tloušťku jen asi 10 km. Pozorování lineárně polarizovaného záření z aktivních jevů nad slunečním limbem mohou být velmi slibná pro stanovení směru vektoru elektrického pole. Tyto zkušenosti a úvahy vedly k sestrojení důmyslného přístroje - elektrografu, instalovaného na velkém koronografu observatoře Sacramento Peak (Moran a Foukal, 1990). Princip elektrografu spočívá v měření profilů čar pomocí rotující půlvlnné destičky a fixně orientovaného lineárního polarizátoru, které jsou umístěny za ohniskem velkého koronografu. Jsou vybrány tak, aby byly účinné v širokém oboru blízké infračervené oblasti, kde se nacházejí čáry Paschenovy série. Záření prošlé touto soustavou je přivedeno přes rotátor obrazu do universálního spektrografu s dispersí 5 Å/mm. Vybrané úseky spektra, obsahující vyšší členy Paschenovy série jsou přivedeny na čip CCD kamery, ochlazovaný na pracovní teplotu kolem -30 °C Peltiérovým efektem v kombinaci se suchým ledem. Proti kondenzaci vody na čipu je použito omývání proudem dusíku. V řídícím počítači je uložena karta - frame grabber, která v rozmezí poloh zadaných operátorem provede časovou integraci signálu spektra z čipu při nastaveném úhlu půlvlnné destičky. Tento proces se zpravidla opakuje pro 12 pozičních úhlů, tedy pro škálu úhlů po 30°. Integrační doby mohou činit pro velmi jasné jevy (koronální kondenzace) řádově sekundy až po desítky sekund u klidných protuberancí. Délka expozice obecně záleží na jasnosti vybrané čáry a momentální průzračnosti vzdušné vrstvy.
Dosavadní měření pomocí elektrografu přinesla některé zajímavé poznatky o emisních čarách vysokých členů Paschenovy série v klidných protuberancích, erupčních smyčkách i koronálních kondenzacích. Zatím se však nepodařilo průkazně změřit hodnoty elektrického pole v těchto aktivních jevech.

Kuželovitá kopule velkého koronografu na observatoři Sacramento Peak, kde byl namontován v r. 1991 elektrograf.
Měření elektrických polí na Slunci - možnosti a problémy
Dostatečně průhledným a spolehlivým principem pro měření elektrických polí dálkovým sondováním je lineární Starkův jev. Ten nastává pouze u vodíkových a vodíku podobných atomů a iontů. Posuny komponent rozštěpených lineárním jevem jsou řádově 100× větší než je tomu u kvadratického Starkova efektu, který se vyskytuje u všech ostatních atomů a iontů. Budeme se proto dále zabývat lineárním efektem. Shrneme si, že rozštěp čáry ve vlnových délkách je přímoúměrný hodnotě elektrického pole E, kvadrátu samotné vlnové délky a kvadrátu hlavního kvantového čísla horní hladiny pro daný přechod elektronu v atomu. Z těchto důvodů se pro měření vybírají vysoké členy sérií vodíku s dlouhými vlnovými délkami okolo 8500 Å (vysoké členy Paschenovy série). Pokud jde o polarizaci záření, komponenty odpovídající přechodům, pro něž je změna magnetického kvantového čísla, Δm = 0 (pí-komponenty), mají lineární polarizaci rovnoběžnou s vektorem elektrického pole E. Sigma-komponenty odpovídají změně Δm ± 1 a mají lineární polarizaci záření kolmou na vektor elektrického pole E.
Hlavní problémy, s nimiž se měření elektrických polí potýká, spočívají zejména v teoretické rovině. Stále častěji se v této souvislosti setkáváme s názory na oprávněnost použití magnetohydrodynamického přiblížení pro fyzikální podmínky ve sluneční atmosféře.
I v případě, že bychom tyto výhrady ignorovali, snadno nahlédneme, že procesy generující elektrická pole ve sluneční plazmě jsou natolik složité, že jsou známy jen odhady jejich průběhu a vlivu na chování elektrických polí. Jednou z vážných pochybností o tom, zda je vůbec možno elektrická pole ve sluneční plazmě měřit, je otázka elektrické vodivosti. Pokud by elektrická vodivost byla natolik veliká, že by se rozdíly potenciálů rychle vyrovnávaly elektrickými proudy, pak bychom stěží mohli očekávat přítomnost jiných elektrických polí než těch, která jsou výsledkem malých fluktuací elektrického náboje. Taková pole by se projevovala v prostoru ohraničeném debyeovským poloměrem. Tím narážíme na druhou obtíž, kterou je velikost dostatečné míry emise v plazmatu ovlivněné elektrickým polem. Dokážeme si představit silné elektrické pole v ohraničeném prostoru plazmy, kde je však míra emise natolik malá, že se starkovský jev na měření profilu čáry vůbec neprojeví. Podobná je i otázka charakteristických časů, po které se elektrická pole ve sluneční atmosféře vyskytují. Pokud by elektrická pole měla trvání kratší nebo srovnatelné s běžnými časy expozic, pak je jen velmi malá pravděpodobnost, že budou detekována.
I když celá řada naměřených výsledků byla interpretována autory jako změřené elektrické pole, zůstává stále otevřenou otázkou, zda se skutečně jedná o elektrické pole, či nějaký jiný efekt. Tím větším dobrodružstvím je možnost zúčastnit se bádání v dosud neprozkoumaném oboru sluneční fyziky.
Zkušenosti z měření elektrografem
Na pozvání Dr. Petra Foukala z CRI, (Cambridge, USA) jsem se v r. 1991 zúčastnil tříměsíčního pobytu na observatoři Sacramento Peak, Nové Mexiko, USA. Z pozorování na elektrografu instalovaném na velkém koronografu jsem získal zkušenost, že jde o přístroj navržený a realizovaný tak, aby minimalizoval rizika možných nezdarů, jejichž příčiny jsou shrnuty v předchozím textu. Navíc měřením polarizace ve 12-ti pozičních úhlech umožňuje určit směr vektoru elektrického pole v rovině kolmé k pozorovací přímce.
Citlivost přístroje byla prokázána mj. pozorováním velmi vysokých členů Paschenovské série až do čáry Paschen 26 v klidných protuberancích Kotrč (1998). Pozorování erupcí na disku, nebo v těsné blízkosti okraje slunečního disku bývá ve slabých čarách natolik ovlivněno rozptýleným světlem disku, že redukce zpravidla nepřichází v úvahu. Při pozorování smyček slunečních erupcí nad slunečním limbem se v pozorovaném vzorku téměř dvaceti erupcí na limbu nenalezl ani jediný případ erupce, která by byla v emisi viditelná ve vyšším členu Paschenovy série než Paschen 16-17. Hlavním problémem u těchto erupcí byla nutnost dlouhých expozičních dob v důsledku poměrně slabé emise a to dokonce i u nižších členů Paschenovy série. V případě pozorování velmi jasného jevu, jakým byla koronální kondenzace, kdy stačily k dosažení poměru signálu k šumu 200 jen půlvteřinové expozice, nastal problém s přílišnou dynamičností tohoto aktivního jevu. I v průběhu série tak krátkých expozic byl patrný přechod jednotlivých vláken kondenzace přes štěrbinu spektrografu. Výsledný profil byl sestaven z několika dopplerovsky posunutých profilů jednotlivých pohybujících se vláken koronální kondenzace.
K závěrům z poznatků z pozorovacího pobytu patří doporučení, aby záměnou půlvlnné destičky, lineárního polarizátoru a detekční kamery byl přístroj přestavěn tak, aby mohl pracovat ve vysokých členech Balmerovy série. Tam sice není vlnová délka tak veliká, ale tyto čáry bývají v erupcích pozorovatelné v emisi. Úpravou optického zobrazení ve spektrografu by bylo možné dosáhnout současné registrace emisního profilu čáry a hladiny rozptýleného světla, což by zvýšilo pravděpodobnost změřit i slabší erupce.
Další z obecně uvažovaných možností detekce elektrických polí na Slunci je přestavět univerzální dvojlomný filtr observatoře Sacramento Peak tak, aby byl účinný ve vlnových délkách vysokých balmerovských čar. Zpracování snímků erupce nebo eruptivní protuberance pořízených v různých směrech polarizace by mohlo vést k informaci o elektrickém poli.
V souhrnu lze konstatovat, že měřitelné hodnoty elektrického pole na Slunci se nepochybně realizují v malých geometrických škálách, které dosud nejsou současnými pozorovacími přístroji a metodami dosažitelné. Bude zajímavé počkat si na nově avizovanou knihu Petra Foukala, která se má elektrickými poli na Slunci zabývat.
Literatura:
Připravované akce
Přednáška "Zpráva o zatmění Slunce 21. srpna"
16. 10. 2017, 19:00 hodin, Zlín
Vyhledávání
Novinky a aktuality
Částečné zatmění Slunce
12.10.22
Částečné zatmění Slunce nastane 25. října 2022 Začátek astronomického úkazu (první kontakt) v 11:14:58 SELČ Hvězdárna bude pro veřejnost otevřena od 11:00 do 14:00 hodiny.
Odešel dlouholetý pozorovatel Slunce
16.02.22
Dne 11. února 2022 nás navždy opustil ve věku 73 let náš kamarád a kolega pan František Zloch, dlouholetý aktivní pozorovatel projevů sluneční aktivity na Astronomickém ústavu AV ČR v Ondřejově a popularizátor nejen astronomie.
Jaký je sluneční cyklus č. 25?
10.02.22
Již dva roky (od prosince 2019) je v činnosti sluneční cyklus s pořadovým číslem 25. Jak to vypadá po srovnání lednových údajů s počty slunečních skvrn a co nás může čekat v budoucnu?











